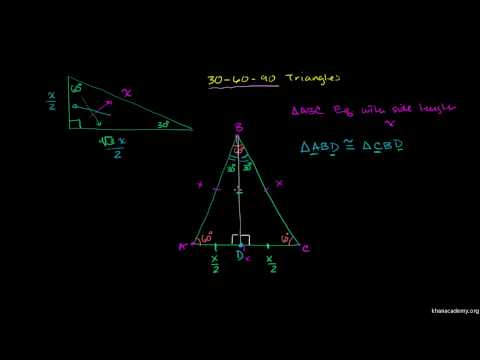
תוֹכֶן
לכל המשולשים הנכונים יש זוויות של 90 מעלות, או זוויות ישרות. הם משמשים במתמטיקה לחישובים מיוחדים, כולל מציאת המרחק המדויק בין שתי נקודות. משולשים ימניים יכולים גם לעזור לכם למצוא גבהים ומרחקים שהם גדולים מאוד או שקשה למדוד אותם בדרך אחרת. למשולשים ימניים יש תכונות מיוחדות רבות המהוות בסיס לטריגונומטריה.
אנטומיה של משולש ימין
שני הצדדים הקצרים יותר של זווית ישרה נקראים רגליים. בדרך כלל הם מסומנים באותיות "a" ו- "b." הצד השלישי, שהוא מול הזווית של 90 מעלות, נקרא היפנוזה ובדרך כלל מסומן כ"ג ".
משפט פיתגורס
משפט פיתגורס קובע כי הסכום של כל אחד משולשי הימני באורך הרגל בריבוע שווה לאורכו של הריבוע המשוחק. במילים אחרות, a ^ 2 + b ^ 2 = c ^ 2, כאשר "a" ו- "b" הם רגליים ו- "c" הוא hypotenuse. אם אתה מכיר שני צדדים במשולש ימני, ניתן להחיל את המשפט כדי למצוא את הצד השלישי. זה משמש במקרים רבים כדי למצוא קושי למדידת מרחקים או אורכים. לדוגמה, אם אתה יודע שאתה נוהג 10 רחובות דרומה, ואז 6 רחובות מזרחה כדי להגיע מהבית לחנות, אך אתה רוצה לדעת מה המרחק הישיר בין הבית לחנות. אתה יכול להגדיר 10 ^ 2 + 6 ^ 2 = (המרחק הישיר) ^ 2 כדי לגלות שזה בערך 12 בלוקים כשהעורב עף.
משולשים 45-45-90
אחד המשולשים הימניים המיוחדים הוא משולש 45-45-90. זה נוצר על ידי ציור קו אלכסוני מפינה אחת לפינה הנגדית של ריבוע. זהו המשולש הימני היחיד בו שתי הרגליים מודדות את אותו אורך בדיוק. לפיכך, זהו הסוג היחיד של המשולש הימני שהוא גם משולש ישר. השם 45-45-90 מגיע ממידות הזוויות הפנימיות שלו. יש את הזווית של 90 מעלות הנדרשת, והזוויות הקטנות יותר מודדות 45 מעלות. הרגליים וההתנפחות תמיד מציגות יחס של 1: √2. לפיכך, עבור משולש זה אתה רק צריך לדעת את האורך של צד אחד כדי למצוא את שני האורכים האחרים. אורכי הרגליים שווים, ואורך ההנפה שווה לאורך הרגל פעמים √2.
משולשים 30-60-90
בדומה למשולש 45-45-90, משולש 30-60-90 מקבל את שמו מכיוון שזוויות הפנים בגודל 30, 60 ו- 90 מעלות. משולש זה נוצר על ידי חיתוך משולש שווה צלעות לחצי. צדי המשולשים 30-60-90 יוצרים גם יחס קבוע של 1: √3: 2. הרגל הקצרה נמצאת ממש מעבר לזווית של 30 מעלות, והיא תמיד מודדת מחצית אורך היפוזה שנמצאת ממול זווית של 90 מעלות. הרגל הארוכה יותר, שנמצאת מעבר לזווית של 60 מעלות, מודדת את אורך זמני הרגל הקצרה √3, או מחצית מהזמנים היפוטוסים √3. לפיכך, עבור משולש זה אתה צריך רק לדעת את האורך של צד אחד כדי למצוא את האורך של שני הצדדים האחרים.