
תוֹכֶן
על מנת ששתי צורות יהיו חופפות, לכל אחת מהן צריך להיות אותו מספר צלעות וזוויותיהם חייבות להיות זהות. הדרכים הקלות ביותר לקבוע אם שתי צורות עומדות בקנה אחד הן לסובב אחת מהצורות עד שהיא עומדת בשורה אחת עם השנייה, או פשוט לערום את הצורות זו על גבי זו כדי לראות אם קצוות כלשהם בולטים. אם אינך מסוגל להזיז את הצורות באופן פיזי, אתה יכול להשתמש בנוסחאות כדי לקבוע אם הצורות הולמות.
מעגלים מתכנסים
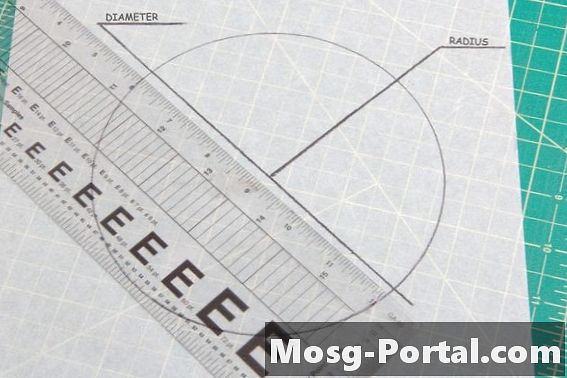
••• ריי רוברט גרין / דרישת מדיהלכל המעגלים אותה זווית של 360 מעלות. הגורם היחיד לקביעת הלימה בין שני מעגלים הוא להשוות את גודלם. הקוטר הוא קו ישר דרך מרכז המעגל מקצה לקצה ואילו רדיוס המעגל הוא האורך ממרכזו לקצה החיצוני. מדידת אחד מאלו בשני המעגלים תוכיח אם הם חופפים.
מקבילים מקבילים
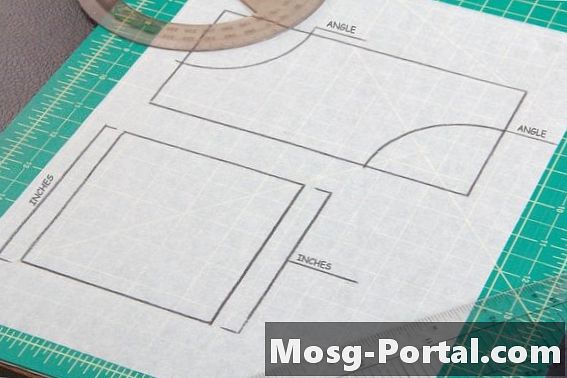
במקביל יש שני זוגות של צדדים מקבילים, כמו ריבועים ומלבנים. הצדדים או הזוויות הנגדיות של מקבילית הם בעלי אותה מידה, ולכן יש צורך לבצע שתי מדידות של זווית או צד על גבי מקביל, אחת מכל זוג צדדים, על מנת להשוות את הלימה לצורה אחרת.
משולשים
••• ריי רוברט גרין / דרישת מדיהעל מנת למצוא את ההתאמה של המשולשים, עליכם לקבוע את הגודל של כל זווית או צד, שכן שלושתם יכולים להיות שונים. ישנן שלוש תנוחות בהן ניתן להשתמש כדי לזהות משולשים חופפים. תנוחת ה- SSS היא כאשר מודדים את כל שלושת הצדדים לכל משולש. המוצא של ASA אומר שאם שני זוויות והצד המחבר שלהם תואמים את זה של המשולש השני, אז הם חופפים. תנוחת SAS עושה את ההפך, מודדת שני צדדים וזווית החיבור שלהם כדי להשוות למשולש השני.
משפטים למשולשים מתכנסים

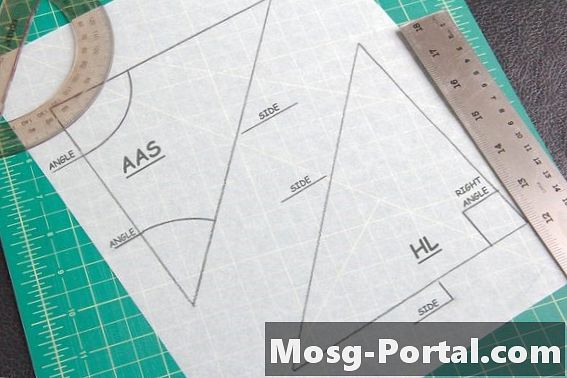
שתי משפטים מועילים למציאת משולשים חופפים. משפט AAS אומר שאם שני זוויות וצד שאינו מחבר בין השניים שווים לזה של משולש אחר, אז הם חופפים. משפט היפוטנוזה-רגל חל רק על משולשים עם זווית אחת של 90 מעלות או "ישרה". זה כאשר אתה מודד את ההיפוטוזה - הצד שמול זווית 90 מעלות - ואת אחד הצדדים האחרים של המשולש, כדי להשוות עם הצורה האחרת.