תוֹכֶן
ניתן להקים מספר מצבים מעניינים בעזרת גלגלות כדי לבחון את התלמידים את ההבנה של חוק התנועה השני של ניוטון, חוק שימור האנרגיה והגדרת העבודה בפיזיקה. ניתן למצוא סיטואציה מאלפת במיוחד ממה שמכונה גלגלת דיפרנציאלית, כלי נפוץ המשמש בחנויות מכונאות להרמה כבדה.
יתרון מכני
בדומה למנוף, הגדלת המרחק שעליו מופעל כוח, בהשוואה למרחק בו מורמים העומס, מגדילה את היתרון המכני, או המינוף. נניח שמשתמשים בשני בלוקים של גלגלות. אחד נצמד לעומס; אחד מצורף למעלה לתמיכה. אם יש להרים את העומס יחידות X, אז גם בלוק הגלגלת התחתון צריך להעלות יחידות X. בלוק הגלגלת למעלה אינו זז למעלה או למטה. לכן המרחק בין שני אבני הגלגלת חייב לקצר יחידות X. אורכי הקו שנמצאים בין שני אבני הגלגלת חייבים כל אחד לקצר את יחידות ה- X. אם ישנם קווים כאלה, על המושך למשוך יחידות X --- Y כדי להרים את יחידות X העומס. כך שהכוח הנדרש הוא פי 1 / Y ממשקל העומס. היתרון המכני אמור להיות Y: 1.
חוק שימור אנרגיה
מינוף זה הוא תוצאה של חוק שימור האנרגיה. נזכיר שעבודה היא סוג של אנרגיה. בעבודה אנו מתכוונים להגדרת הפיזיקה: כוח המופעל על עומס פעמים המרחק עליו מועבר העומס על ידי הכוח. כך שאם העומס הוא Z Newtons, האנרגיה שהוא לוקח להרים את יחידות ה- X חייבת להיות שווה לעבודה שנעשה על ידי הנגר. במילים אחרות, Z --- X חייב להיות שווה (כוח המופעל על ידי מושך) --- XY. לפיכך, הכוח המופעל על ידי המושך הוא Z / Y.
גלגלת דיפרנציאלית
משוואה מעניינת מתעוררת כאשר הופכים את הקו לולאה רציפה, ולגוש התלוי מהתמיכה יש שני גלגלות, האחת קטנה מעט מהשנייה. נניח גם ששני הגלגלים בגוש מחוברים כך שיסובבו זה בזה. קרא לרדיוסים של הגלגלות "R" ו- "r", שם R> r.
אם המושך שולף מספיק קו כדי לסובב את הגלגלים הקבועים דרך סיבוב אחד, הוא שלף 2πR של הקו. הגלגלת הגדולה יותר תפסה אז 2πR של קו מתומך בעומס. הגלגלת הקטנה יותר מסתובבת באותו כיוון, ומשחררת 2πr של קו לעומס. כך העומס עולה 2πR-2πr. היתרון המכני הוא המרחק שנמשך חלקי המרחק שהועלה, או 2πR / (2πR-2πr) = R / (R-r). שימו לב שאם הרדיוסים נבדלים זה מזה בשני אחוזים בלבד, היתרון המכני הוא עצום של 50 ל -1.
גלגלת כזו מכונה גלגלת דיפרנציאלית. זהו מתקן נפוץ בחנויות לתיקוני רכב. יש לו את התכונה המעניינת כי הקו שמושך המושך יכול להשתחרר בזמן שעומס מוחזק למעלה, מכיוון שתמיד יש מספיק חיכוכים לכך שהכוחות המנוגדים בשתי הגלגלות מונעים ממנו להסתובב.
החוק השני של ניוטון


נניח ששני בלוקים מחוברים, ואחד, תקרא לזה M1, תולה מעל הגלגלת. כמה מהר הם יאיצו? החוק השני של ניוטון מתייחס לכוח ולהאצה: F = ma. המסה של שני הבלוקים ידועה (M1 + M2). האצה אינה ידועה. כוח ידוע ממשיכת הכבידה על M1: F = ma = M1 --- g, כאשר g הוא האצת הכבידה על פני כדור הארץ.
זכור כי M1 ו- M2 יואצו יחד. מציאת ההאצה שלהם, א, זה עכשיו רק עניין של החלפה לנוסחה F = ma: M1 --- g = (M1 + M2) א. כמובן שאם החיכוך בין M2 לשולחן הוא אחד הכוחות ש- F = M1 --- g צריך להתנגד להם, אז הכוח הזה מתווסף בקלות גם לצד הימני של המשוואה, לפני שהתאוצה, a, היא נפתר עבור.
עוד בלוקים תלויים

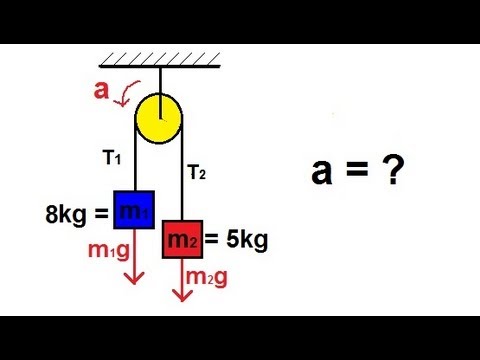
מה אם שני הבלוקים תלויים? ואז בצד שמאל של המשוואה יש שני תוספות במקום רק אחת. הקל יותר ינוע בכיוון ההפוך של הכוח המתקבל, מכיוון שהמסה הגדולה יותר קובעת את כיוון המערכת דו-המונית; לפיכך יש להפחית את כוח הכבידה על המסה הקטנה יותר. נניח M2> M1. ואז הצד השמאלי שלמעלה משתנה מ- M1 --- g ל- M2 --- g-M1 --- g. יד ימין נשארת זהה: (M1 + M2) א. ההאצה, א, נפתרת לאחר מכן בצורה טריוויאלית.