תוֹכֶן
בגיאומטריה מתומן הוא מצולע עם שמונה צדדים. מתומן רגיל יש שמונה צדדים שווים וזוויות שוות. האוקטגון הרגיל מוכר בדרך כלל מסימני עצירה. אוקטהדרון הוא פוליהדרון דו-צדדי. לאוקטאהדרון רגיל שמונה משולשים עם קצוות באורך שווה. מדובר למעשה בשתי פירמידות מרובעות שנפגשות בבסיסן.
פורמולה של אוקטגון
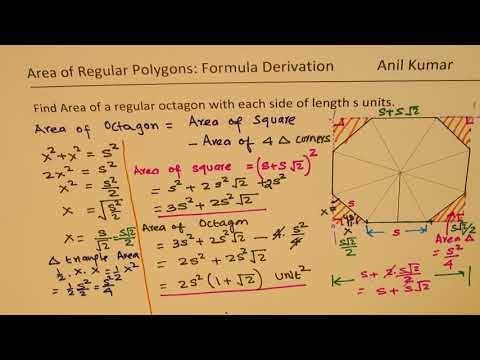
הנוסחה לשטח של מתומן רגיל עם צידי אורך "a" היא 2 (1 + sqrt (2)) a ^ 2, כאשר "sqrt" מציין את השורש הריבועי.
נגזרת
ניתן לראות מתומן כ -4 מלבנים, ריבוע אחד במרכז וארבעה משולשים מרובעים בפינות.
הכיכר היא שטח A ^ 2.
למשולשים יש צדדים a, a / sqrt (2) ו- a / sqrt (2), לפי משפט פיתגורס. לכן לכל אחד מהם שטח של ^ 2/4.
המלבנים הם באזור a * a / sqrt (2).
הסכום של 9 אזורים אלה הוא 2a ^ 2 (1 + מ"ר (2)).
נוסחת נפח של אוקטהדרון
הנוסחה לנפח של אוקטאתדרון רגיל של הצדדים "a" היא ^ 3 * מ"ר (2) / 3.
נגזרת
שטח הפירמידה הארבע צדדית הוא שטח בסיס * גובה / 3. שטח של מתומן רגיל הוא אפוא 2 * בסיס * גובה / 3.
בסיס = a ^ 2 בצורה טריוויאלית.
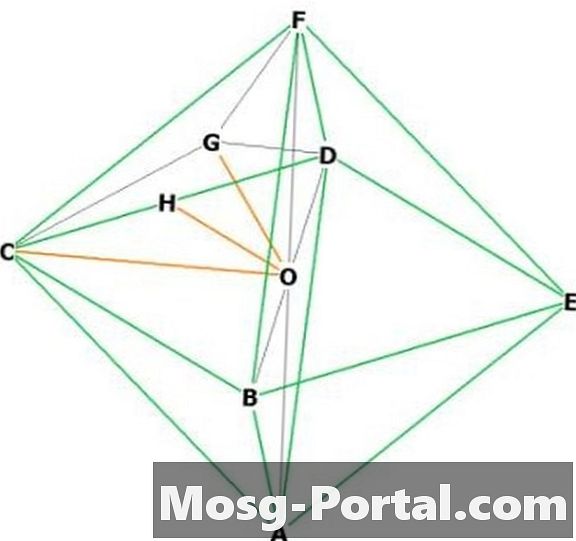
בחרו שני קודקודים סמוכים, אמרו "F" ו- "C." "O" נמצא במרכז. FOC הוא משולש ימין עם שקע ישר עם בסיס "a", כך OC ו- OF יש אורך / sqrt (2) על ידי משפט פיתגורס. אז גובה = a / sqrt (2).
אז הנפח של אוקטאתדרון רגיל הוא 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
שטח פנים
משטח האוקטאהדרון הרגיל הוא שטח משולש שווה צלעות של הצד 'a' פי 8 פנים.
לשימוש במשפט פיתגורס, שחרר קו מהקצה לבסיס. זה יוצר שני משולשים ימניים, עם היפוזה של אורך "a" ואורך צד אחד "a / 2". לכן הצד השלישי חייב להיות sqrt = sqrt (3) a / 2. אז השטח של משולש שווה שוקיים הוא גובה * בסיס / 2 = מ"ר (3) a / 2 * a / 2 = מ"ר (3) a ^ 2/4.
עם 8 צדדים, שטח הפנים של אוקטהדרון רגיל הוא 2 * מ"ר (3) * a ^ 2.