
תוֹכֶן
- נוסחת טעינה חשמלית
- מטען וכוח כוח חשמלי: קווי דמיון
- שימור מטען חשמלי
- מספר האלקטרונים בתשלום
- חישוב מטען חשמלי במעגלים
- נוסחת שדה חשמלי
- המטען נטו של היקום
- חישוב שטף חשמלי בתשלום
- טעינה וחשמל סטטי
- מוליכים חשמליים
- חוק גאוס במצבים אחרים
בין אם החשמל הסטטי המוענק על ידי מעיל פרוותי או החשמל המניע מכשירי טלוויזיה, תוכלו ללמוד עוד על מטען חשמלי על ידי הבנת הפיזיקה העומדת בבסיס. השיטות לחישוב המטען תלויות באופי החשמל עצמו, כמו עקרונות כיצד המטען מפיץ את עצמו באמצעות עצמים. עקרונות אלה זהים לא משנה היכן אתה נמצא ביקום, מה שהופך מטען חשמלי לנכס בסיסי של המדע עצמו.
נוסחת טעינה חשמלית
ישנן דרכי חישוב רבות מטען חשמלי עבור חסרונות שונים בפיזיקה והנדסת חשמל.
חוק קולומבס משמש בדרך כלל בעת חישוב הכוח הנובע מחלקיקים הנושאים מטען חשמלי, והוא אחת ממשוואות המטען החשמלי הנפוצות ביותר בהן תשתמשו. אלקטרונים נושאים מטענים פרטניים של -1602 × 10-19 coulombs (C), ופרוטונים נושאים אותה כמות, אך בכיוון החיובי, 1.602 × 10 −19 ג. לשני חיובים ש1 ו ש2 _ זה מופרדים על ידי מרחק _r, אתה יכול לחשב את הכוח החשמלי וה שנוצר באמצעות חוק קולומבס:
F_E = frac {kq_1q_2} {r ^ 2}בו k הוא קבוע k = 9.0 × 10 9 נ.מ.2 / ג2. פיזיקאים ומהנדסים משתמשים לפעמים במשתנה ה להתייחס לטעינה של אלקטרון.
שימו לב, עבור מטענים של סימנים הפוכים (פלוס מינוס), הכוח שלילי ולכן מושך בין שני המטענים. עבור שני מטענים של אותו סימן (פלוס פלוס או מינוס ומינוס), הכוח דוחה. ככל שהמטענים גדולים יותר, כך כוחם האטרקטיבי או הדוחה יותר חזק ביניהם.
מטען וכוח כוח חשמלי: קווי דמיון
חוק קולומבס נושא דמיון רב לחוק הניוטונים בכוח הכבידה וז = G m1M2 / r2 לכוח הכבידה וז, המונים M1ו M2, וקבוע כבידה ז = 6.674 × 10 −11 M3ק"ג2. שניהם מודדים כוחות שונים, משתנים עם מסה או מטען גדולים יותר ותלויים ברדיוס בין שני העצמים לכוח השני. למרות הדמיון, חשוב לזכור את כוחות הכבידה הם תמיד מושכים בעוד כוחות חשמליים יכולים להיות מושכים או דוחים.
עליכם לציין כי הכוח החשמלי בדרך כלל חזק בהרבה מכוח הכבידה על סמך ההבדלים בכוח האקספוננציאלי של קבועי החוקים. קווי הדמיון בין שני חוקים אלה מהווים אינדיקציה גדולה יותר לסימטריה ודפוסים בקרב חוקי היקום הנפוצים.
שימור מטען חשמלי
אם מערכת תישאר מבודדת (כלומר ללא קשר עם שום דבר אחר שמחוצה לה), היא תחסוך טעינה. שימור תשלום פירושו שכמות המטען החשמלי הכוללת (מטען חיובי פחות טעינה שלילית) נותרה זהה למערכת. שימור מטען מאפשר לפיזיקאים ומהנדסים לחשב כמה טעינה נעה בין מערכות לסביבתם.
עיקרון זה מאפשר למדענים ומהנדסים ליצור כלובי פאראדיי המשתמשים במגנים מתכתיים או בציפוי כדי למנוע את בריחת המטען. כלובי פאראדיי או מגני פאראדיי משתמשים בנטייה לשדות חשמליים להפצה מחדש של מטענים בתוך החומר כדי לבטל את השפעת השדה ולמנוע מהמטענים לפגוע או להיכנס לפנים. אלה משמשים בציוד רפואי כמו מכונות הדמיה לתהודה מגנטית, למניעת עיוות נתונים, ובכלי הגנה לחשמלאים ולסתמים העובדים בסביבות מסוכנות.
אתה יכול לחשב את זרימת המטען נטו עבור נפח שטח על ידי חישוב הסכום הכולל של המטען שנכנס ומחסר את הסכום הכולל של טעינה שנותרה. באמצעות אלקטרונים ופרוטונים הנושאים מטען, ניתן ליצור או להרוס חלקיקים טעונים כדי לאזן את עצמם בהתאם לשימור המטען.
מספר האלקטרונים בתשלום
בידיעה שהמטען של אלקטרון הוא -1602 × 10 −19 C, מטען של 8 × 10 −18 C יהיה מורכב מ- 50 אלקטרונים. אתה יכול למצוא זאת על ידי חלוקת כמות המטען החשמלי בעוצמת המטען של אלקטרון בודד.
חישוב מטען חשמלי במעגלים
אם אתה יודע זרם חשמלי, זרימת מטען חשמלי דרך אובייקט, נסיעה במעגל וכמה זמן מוחל הזרם, ניתן לחשב מטען חשמלי באמצעות המשוואה לזרם ש = זה בו ש הוא המטען הכולל שנמדד בקולומבים, אני הוא הנוכחי במגברים, ו- t זה הזמן שהזרם מוחל תוך שניות. אתה יכול גם להשתמש בחוק אוהם (V = IR) לחישוב זרם מתח ומתנגדות.
עבור מעגל עם מתח 3 וולט והתנגדות 5 Ω המופעל במשך 10 שניות, הזרם המקביל שמתקבל הוא אני = V / ר = 3 V / 5 Ω = 0.6 A, והמטען הכולל יהיה ש = זה = 0.6 A × 10 ש '= 6 צ.
אם אתה יודע מה ההבדל הפוטנציאלי (V) בוולט המיושם במעגל ובעבודה (W) בג'ואלים שנעשו במהלך התקופה שהיא מיושמת, המטען בקולומבים, ש = W / V.
נוסחת שדה חשמלי
•שדה חשמלי, הכוח החשמלי לטעינת יחידה, מתפשט באופן רדיאלי כלפי מטען חיובי לכיוון מטענים שליליים וניתן לחשב אותו בעזרת ה = וה / ש, בו וה הוא הכוח החשמלי ו ש הוא המטען שמייצר את השדה החשמלי. בהתחשב באיזו מידה שדה וכוח בסיסי לחישובים בחשמל ומגנטיות, מטען חשמלי עשוי להיות מוגדר כמאפיין של חומר הגורם לחלקיק להיות בעל כוח בנוכחות שדה חשמלי.
גם אם המטען נטו, או סה"כ, על אובייקט הוא אפס, שדות חשמליים מאפשרים חלוקת מטענים בגינונים שונים בתוך עצמים. אם יש בתוכם חלוקות מטען המביאות למטען נטו שאינו אפס, אובייקטים אלה הם מקוטב, והחיוב שנגרם לקיטוב אלה מכונה חיובים כבולים.
המטען נטו של היקום
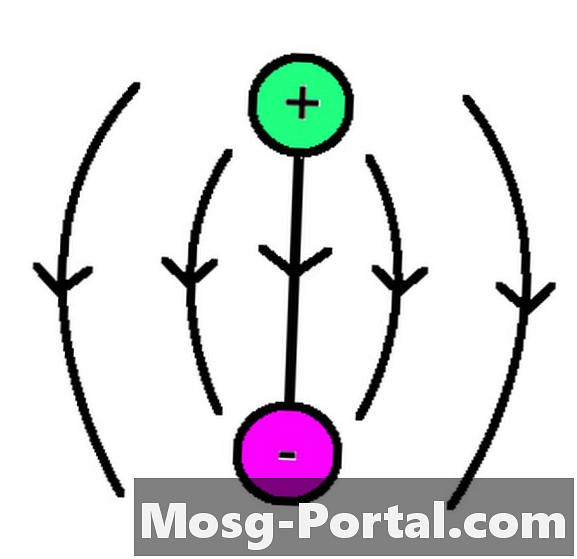
אף על פי שמדענים לא מסכימים כולם על הטעינה הכוללת של היקום, הם עשו ניחושים משכילים ובחנו השערות בשיטות שונות. יתכן שתבחין כי כוח הכבידה הוא הכוח הדומיננטי ביקום בסולם הקוסמולוגי, ומכיוון שהכוח האלקטרומגנטי הוא הרבה יותר חזק מכוח הכבידה, אם ליקום היה מטען נטו (חיובי או שלילי), היית מסוגל ראה ראיות לכך במרחקים כה גדולים. היעדר עדות זו הביא את החוקרים להאמין שהיקום הוא ניטרלי מטען.
אם היקום תמיד היה ניטרלי טעינה או כיצד המטען של היקום השתנה מאז המפץ הגדול הם גם שאלות שעומדות לדיון. אם ליקום היה מטען נטו, מדענים צריכים להיות מסוגלים למדוד את נטיותיהם והשפעותיהם על כל קווי השדה החשמל באופן כזה שבמקום להתחבר ממטענים חיוביים למטענים שליליים, הם לעולם לא ייגמרו. היעדר תצפית זו מצביע גם על הטענה כי ליקום אין מטען נטו.
חישוב שטף חשמלי בתשלום
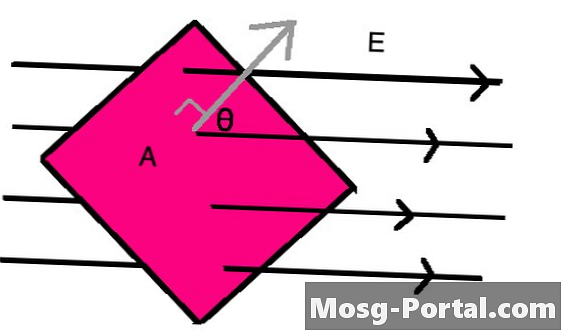
•ה שטף חשמלי דרך שטח מישורי (כלומר שטוח) א של שדה חשמלי ה הוא השדה כפול רכיב השטח הניצב לשדה. כדי להשיג רכיב אנכי זה, אתה משתמש בקוסינוס של הזווית בין השדה ומישור העניין בנוסחה לשטף, המיוצג על ידי Φ = EA cos (θ), איפה θ הוא הזווית בין הקו הניצב לאזור לכיוון השדה החשמלי.
משוואה זו, המכונה חוק גאוס, גם אומר לך שעבור משטחים כמו אלה שאתה קורא להם משטחים גאוסיים, כל מטען נטו היה שוכן על פני השטח של המטוס מכיוון שהיה צורך ליצור את השדה החשמלי.
מכיוון שהדבר תלוי בגיאומטריה של שטח המשטח המשמש בחישוב שטף, זה משתנה בהתאם לצורה. עבור אזור מעגלי, אזור השטף א יהיה π_r_2 עם r כרדיוס המעגל, או עבור המשטח המעוגל של הצילינדר, שטח השטף יהיה Ch בו ג הוא היקף פני הגליל העגול ו ח הוא גובה הצילינדרים.
טעינה וחשמל סטטי
חשמל סטטי מופיע כששני עצמים אינם בשיווי משקל חשמלי (או שיווי משקל אלקטרוסטטי), או שיש זרימה נטו של מטענים מאובייקט אחד למשנהו. כאשר חומרים מתחככים זה בזה, הם מעבירים מטענים זה בזה. שפשוף גרביים על שטיח או גומי של בלון מנופח על שיערך יכולים לייצר צורות חשמל אלה. ההלם מעביר את המטענים העודפים האלה בחזרה, כדי לבסס מחדש מצב של שיווי משקל.
מוליכים חשמליים
למשך מנצח (חומר שמעביר חשמל) בשיווי משקל אלקטרוסטטי, השדה החשמלי בפנים הוא אפס והמטען הנקי על פני השטח שלו חייב להישאר בשיווי משקל אלקטרוסטטי. הסיבה לכך היא שאם היה שדה, האלקטרונים במוליך היו מפיצים או מיישרים עצמם מחדש בתגובה לשדה. בדרך זו הם יבטלו כל שדה ברגע שייווצר.
חוטי אלומיניום ונחושת הם חומרי מוליך נפוצים המשמשים להעברת זרמים, ולעיתים קרובות משמשים גם מוליכים יוניים, שהם פתרונות המשתמשים ביונים צפים בחופשיות כדי לאפשר לטעינה לעבור בקלות. מוליכים למחצה, כמו השבבים המאפשרים למחשבים לתפקד, משתמשים גם באלקטרונים המסתובבים חופשי, אך לא רבים כמו שמוליכים עושים. מוליכים למחצה כמו סיליקון וגרמניום דורשים גם יותר אנרגיה כדי לאפשר למטענים להסתובב ובאופן כללי יש מוליכות נמוכה. בניגוד, מבודדים כגון עץ לא מאפשרים לטעון בקלות דרכם.
ללא שדה בפנים, עבור משטח גאוסי שנמצא ממש בתוך משטח המוליך, השדה צריך להיות אפס בכל מקום כך שטף האפס. המשמעות היא שאין מטען חשמלי נטו בתוך המוליך. מכאן תוכלו להסיק כי עבור מבנים גיאומטריים סימטריים כמו כדורים, המטען מתפזר באופן אחיד על פני השטח של הגאוס.
חוק גאוס במצבים אחרים
מכיוון שהמטען הנקי על משטח חייב להישאר בשיווי משקל אלקטרוסטטי, כל שדה חשמלי חייב להיות בניצב לפני השטח של המוליך כדי לאפשר לחומר להעביר מטענים. חוק גאוס מאפשר לך לחשב את גודל השדה החשמלי הזה ואת השטף עבור המוליך. השדה החשמלי בתוך המוליך חייב להיות אפס, ובחוץ, עליו להיות בניצב לפני השטח.
משמעות הדבר היא שמוליך גלילי עם שדה הקורן מהקירות בזווית אנכית, השטף הכולל הוא פשוט 2_E__πr_2 לשדה חשמלי ה ו r רדיוס הפנים המעגל של המוליך הגלילי. אתה יכול גם לתאר את המטען נטו על פני השטח באמצעות σ, ה צפיפות מטען לכל שטח יחידה, כפול השטח.