הלכות תנועה מטוטלת

תוֹכֶן

• TL; DR (יותר מדי זמן; לא קרא)
• תנועה הרמונית פשוטה
• חוקים של מטוטלת פשוט
• נגזרת מטוטלת פשוט
• גורמים המשפיעים על תנועת המטוטלת
• אורך המטוטלת דוגמה
• הגדרת מטוטלת פשוטה
• חוקים בניוטונים במטוטלות

למטוטלות תכונות מעניינות בהן משתמשים פיזיקאים כדי לתאר עצמים אחרים. לדוגמה, מסלול פלנטרי עוקב אחר דפוס דומה והתנודדות על ערכת נדנדה עשויה להרגיש כמו שאתה על מטוטלת. תכונות אלה נובעות מסדרת חוקים השולטים בתנועת המטוטלת. על ידי לימוד חוקים אלה, אתה יכול להתחיל להבין כמה מהיסודות הבסיסיים של הפיזיקה והתנועה בכלל.

TL; DR (יותר מדי זמן; לא קרא)

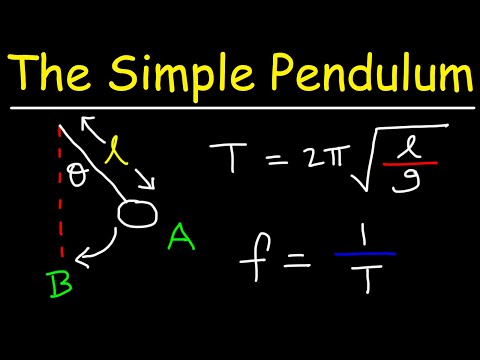
ניתן לתאר את תנועת המטוטלת באמצעות θ (t) = θ_{מקסימום}cos (2πt / T) בו θ מייצג את הזווית בין המיתר לקו האנכי במורד המרכז, t מייצג זמן, ו ט היא התקופה, הזמן הדרוש כדי להתרחש מחזור שלם אחד של תנועת המטוטלת (נמדד על ידי 1 / f), של תנועת המטוטלת.

תנועה הרמונית פשוטה

תנועה הרמונית פשוטה, או תנועה המתארת ​​כיצד מהירות עצמים מתנדנדת ביחס לכמות העקירה משיווי משקל, ניתן להשתמש כדי לתאר את המשוואה של מטוטלת. בוב מסתובב מטוטלת נשמר בתנועה על ידי כוח זה הפועל עליו כשהוא נע קדימה ואחורה.

••• סיד חוסיין אתר

החוקים השולטים בתנועת המטוטלת הובילו לגילוי נכס חשוב. פיזיקאים מפרקים כוחות למרכיב אנכי ורכיב אופקי. בתנועת מטוטלת, שלושה כוחות פועלים ישירות על המטוטלת: מסת הבוב, כוח המשיכה והמתח במיתר. מסה וכוח כוח שניהם עובדים אנכית כלפי מטה. מכיוון שהמטוטלת אינה נעה מעלה או מטה, הרכיב האנכי של מתח המיתרים מבטל את המסה וכוח המשיכה.

זה מראה שמסת המטוטלת אינה רלוונטית לתנועתה, אך מתח המיתרים האופקיים כן. תנועה הרמונית פשוטה דומה לתנועה מעגלית. ניתן לתאר אובייקט הנע בנתיב מעגלי כפי שמוצג באיור למעלה על ידי קביעת הזווית והרדיוס שהוא לוקח בנתיב העגול המקביל שלו. ואז, בעזרת הטריגונומטריה של המשולש הימני בין מרכז המעגלים, מיקום האובייקטים והעקירה בשני הכיוונים x ו- y, תוכלו למצוא משוואות x = rsin (θ) ו y = rcos (θ).

המשוואה החד מימדית של אובייקט בתנועה הרמונית פשוטה ניתנת על ידי x = r cos (ωt). אתה יכול להחליף עוד יותר א ל r בו א האם ה אמפליטודה, העקירה המרבית מהמיקום הראשוני של האובייקטים.

המהירות הזוויתית ω ביחס לזמן t לזוויות אלה θ ניתן ע"י θ = ωt. אם תחליף את המשוואה המתייחסת למהירות הזוויתית לתדר ו, ω = 2πf_, אתה יכול לדמיין את התנועה הסיבובית הזו, ואז, כחלק ממטוטלת המתנדנדת קדימה ואחורה, אז משוואת התנועה ההרמונית הפשוטה המתקבלת היא _x = A cos (2πft).

חוקים של מטוטלת פשוט

••• סיד חוסיין אתר

מטוטלות, כמו המונים על מעיין, הן דוגמאות ל מתנדים הרמוניים פשוטים: יש כוח המשחזר שמתגבר תלוי עד כמה העקירה של המטוטלת ניתן לתאר את תנועתם באמצעות משוואת מתנד הרמונית פשוטה θ (t) = θ_{מקסימום}cos (2πt / T) בו θ מייצג את הזווית בין המיתר לקו האנכי במורד המרכז, t מייצג זמן ו ט האם ה פרק זמן, הזמן הדרוש כדי להתרחש מחזור שלם אחד של תנועת המטוטלת (נמדד על ידי 1 / f), של תנועת המטוטלת.

θ_{מקסימום} היא דרך נוספת להגדיר את המקסימום שהזווית מתנדנדת במהלך תנועת המטוטלת והיא דרך נוספת להגדרת משרעת המטוטלות. שלב זה מוסבר להלן תחת הסעיף "הגדרת מטוטלת פשוטה."

השלכה נוספת של חוקי המטוטלת הפשוטה היא שתקופת התנודה באורך קבוע אינה תלויה בגודל, בצורה, במסה ובחומר של האובייקט בקצה המיתר. זה מוצג בבירור דרך נגזרת המטוטלת הפשוטה והמשוואות שמתקבלות.

נגזרת מטוטלת פשוט

אתה יכול לקבוע את המשוואה עבור א מטוטלת פשוטה, ההגדרה התלויה במתנד הרמוני פשוט, מסדרת שלבים המתחילים במשוואת התנועה למטוטלת. מכיוון שכוח הכובד של מטוטלת שווה לכוח של תנועת המטוטלת, אתה יכול להגדיר אותם שווים אחד לשני באמצעות החוק השני של ניוטון עם מסת מטוטלת M, אורך המחרוזת ל, זווית θ, תאוצה כבידה ז ומרווח זמן t.

••• סיד חוסיין אתר

אתה קובע את החוק השני של ניוטון שווה לרגע האינרציה אני = מר²_כמה המוני _m ורדיוס התנועה הסיבובית (אורך המיתר במקרה זה) r פעמים ההאצה הזוויתית α.

ישנן דרכים אחרות ליצור נגזרת מטוטלת פשוטה. להבין את המשמעות שמאחורי כל שלב כדי לראות כיצד הם קשורים. אתה יכול לתאר תנועה מטוטלת פשוטה באמצעות תיאוריות אלה, אך עליך לקחת בחשבון גם גורמים אחרים שעשויים להשפיע על תורת המטוטלת הפשוטה.

גורמים המשפיעים על תנועת המטוטלת

אם תשווה את התוצאה של נגזרת זו θ (t) = θ_{מקסימום}cos (t (L / g)²) למשוואה של מתנד הרמוני פשוט (_θ (t) = θ_{מקסימום}cos (2πt / T)) b_y הגדרת אותם שווים זה לזה, אתה יכול לגזור משוואה לתקופה T.

שימו לב שמשוואה זו T = 2π (L / g)^-1/2 לא תלוי במסה M של המטוטלת, המשרעת θ_{מקסימום}, וגם לא בזמן t. המשמעות היא שהתקופה אינה תלויה במסה, במשרעת ובזמן, אך במקום זאת מסתמכת על אורך המיתר. זה נותן לך דרך תמציתית להביע תנועת מטוטלת.

אורך המטוטלת דוגמה

עם המשוואה לתקופה T = 2π (L / g) __^-1/2, אתה יכול לארגן מחדש את המשוואה לקבלת L = (T / 2_π)² / g_ ומחליפים 1 שניות עבור ט ו 9.8 מ '/ ש² ל ז להשיג L = 0.0025 מ '. קחו בחשבון שמשוואות אלה של תורת המטוטלות הפשוטות מניחות שאורך המיתר הוא חסר חיכוך וחסר מסה. כדי לקחת בחשבון גורמים אלה ידרוש משוואות מורכבות יותר.

הגדרת מטוטלת פשוטה

אתה יכול למשוך את הזווית המטוטלת לאחור θ לתת לו להתנדנד קדימה ואחורה לראות שהוא מתנדנד ממש כמו קפיץ עשוי. למטוטלת פשוטה ניתן לתאר אותה באמצעות משוואות תנועה של מתנד הרמוני פשוט. משוואת התנועה עובדת טוב לערכים קטנים יותר של זווית ו אמפליטודה, הזווית המרבית, מכיוון שמודל המטוטלת הפשוט מסתמך על הקירוב ש חטא (θ) ≈ θ לזווית מטוטלת כלשהי θ. ככל שזוויות הערך והמשרעות הופכות לגדולות מכ 20 מעלות, קירוב זה לא עובד גם כן.

נסה זאת בעצמך. מטוטלת המתנדנדת עם זווית ראשונית גדולה θ לא מתנדנד כמו באופן קבוע כדי לאפשר לך להשתמש במתנד הרמוני פשוט כדי לתאר את זה. בזווית ראשונית קטנה יותר θהמטוטלת מתקרבת לתנועה מתנדנדת רגילה בהרבה יותר קל. מכיוון שמסת המטוטלת אינה משפיעה על תנועתה, פיזיקאים הוכיחו שלכל המטוטלות יש את אותה התקופה לזוויות תנודה - הזווית בין מרכז המטוטלת בנקודה הגבוהה ביותר למרכז המטוטלת במצבה העצור - פחות מעל 20 מעלות.

לכל המטרה הפרקטית של מטוטלת בתנועה, המטוטלת תידרש בסופו של דבר ותיעצר בגלל החיכוך בין המיתר לנקודת ההידוק שלו למעלה כמו גם בגלל עמידות האוויר בין המטוטלת והאוויר סביבו.

עבור דוגמאות מעשיות לתנועת המטוטלת, התקופה והמהירות היו תלויים בסוג החומר המשמש שיגרום לדוגמאות אלה לחיכוך והתנגדות אוויר. אם תבצעו חישובים על התנהגות מתנדנדת מטוטלת תיאורטית מבלי לתת דין וחשבון על הכוחות הללו, זה יהווה מטוטלת המתנדנדת עד אין קץ.

חוקים בניוטונים במטוטלות

החוק הראשון של ניוטון מגדיר את מהירות העצמים בתגובה לכוחות. החוק קובע כי אם חפץ יעבור במהירות ספציפית ובקו ישר, הוא ימשיך לנוע באותה מהירות ובקו ישר, אין סופי, כל עוד שום כוח אחר לא יפעל עליו. דמיין שזורק כדור ישר קדימה - הכדור היה מסתובב סביב כדור הארץ שוב ושוב אם התנגדות האוויר וכוח הכבידה לא היו פועלים עליו. חוק זה מראה שמכיוון שמטוטלת נעה זו לצד זו ולא מעלה ומטה אין לה כוחות מעלה ומטה הפועלים עליו.

החוק השני של ניוטון משמש לקביעת הכוח הנקי על המטוטלת על ידי קביעת כוח הכבידה שווה לכוח המיתר שמושך בחזרה כלפי מטוטלת. הגדרת משוואות אלה שוות זו לזו מאפשרת לך להפיק את משוואות התנועה של המטוטלת.

החוק השלישי של ניוטון קובע שלכל פעולה יש תגובה של כוח שווה. חוק זה עובד עם החוק הראשון שמראה שלמרות שהמסה וכוח הכבידה מבטלים את המרכיב האנכי של וקטור מתח המיתר, שום דבר לא מבטל את הרכיב האופקי. חוק זה מראה כי הכוחות הפועלים על מטוטלת יכולים לבטל זה את זה.

פיזיקאים משתמשים בניוטונים בחוקים ראשונים, שניים ושלישיים כדי להוכיח את המתח המיתרי האופקי מזיז את המטוטלת ללא התחשבות במסה או בכוח המשיכה. חוקי המטוטלת הפשוטה עוקבים אחר רעיונותיהם של שלושת חוקי התנועה של ניוטון.