תוֹכֶן
שלוש השיטות הנפוצות ביותר לפתרון מערכות משוואה הן החלפה, חיסול ומטריצות מוגדלות. החלפה וחיסול הן שיטות פשוטות שיכולות לפתור ביעילות את רוב המערכות של שתי משוואות בכמה צעדים פשוטים. שיטת המטריצות המוגדלות דורשת צעדים רבים יותר, אך יישומה נמשך למגוון גדול יותר של מערכות.
החלפה
החלפה היא שיטה לפתרון מערכות משוואות על ידי הסרת כל אחד מהמשתנים פרט לאחד ומשוואות ואז פתרון משוואה זו. זה מושג על ידי בידוד המשתנה האחר במשוואה ואז החלפת ערכים על משתנים אלה במשוואה אחרת אחרת. לדוגמה, כדי לפתור את מערכת המשוואות x + y = 4, 2x - 3y = 3, בידדו את המשתנה x במשוואה הראשונה כדי לקבל x = 4 - y, ואז החליפו ערך זה של y למשוואה השנייה כדי לקבל 2 (4 - y) - 3y = 3. משוואה זו מפשטת ל- -5y = -5, או y = 1. חבר ערך זה למשוואה השנייה כדי למצוא את הערך של x: x + 1 = 4 או x = 3.
חיסול
חיסול הוא דרך נוספת לפתור מערכות של משוואות על ידי שכתוב אחת המשוואות במונחים של משתנה אחד בלבד. שיטת החיסול משיגה זאת על ידי הוספה או חיסור של משוואות זו מזו על מנת לבטל את אחד המשתנים. לדוגמא, הוספת המשוואות x + 2y = 3 ו- 2x - 2y = 3 מניבה משוואה חדשה, 3x = 6 (שימו לב שתנאי y התבטלו). לאחר מכן המערכת נפתרת באותה שיטות כמו להחלפה. אם אי אפשר לבטל את המשתנים במשוואות, יהיה צורך להכפיל את המשוואה כולה בגורם בכדי לגרום להתאמת המקדמים.
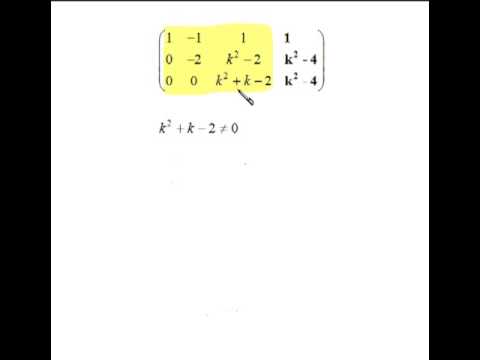
מטריקס מוגדל
מטריות מוגדלות יכולות לשמש גם לפתרון מערכות משוואות. המטריצה המוגדלת מורכבת משורות לכל משוואה, עמודות לכל משתנה ועמודה מוגברת המכילה את המונח הקבוע בצד השני של המשוואה. לדוגמה, המטריצה המוגברת עבור מערכת המשוואות 2x + y = 4, 2x - y = 0 היא, ...].
קביעת הפיתרון
השלב הבא כולל שימוש בפעולות שורה אלמנטריות כמו הכפלת או חלוקת השורה בקבוע שאינו אפס והוספת או חיסור שורות. מטרת פעולות אלה היא להמיר את המטריצה לצורת דרג שורה, בה הרשומה הראשונה שאינה אפס בכל שורה היא 1, הערכים מעל ומתחת לערך זה כולם אפסים, והערך הראשון שאינו אפס לכל אחד השורה נמצאת תמיד מימין לכל הרשומות מסוג זה בשורות שמעליה. צורת הדרג למטריצה לעיל היא, ...]. הערך של המשתנה הראשון ניתן על ידי השורה הראשונה (1x + 0y = 1 או x = 1). הערך של המשתנה השני ניתן על ידי השורה השנייה (0x + 1y = 2 או y = 2).
יישומים
החלפה וחיסול הן שיטות פשוטות יותר לפתרון משוואות ומשתמשות בתדירות גבוהה בהרבה מאשר מטריצות מוגברות באלגברה בסיסית. שיטת ההחלפה מועילה במיוחד כאשר אחד המשתנים כבר מבודד באחת המשוואות. שיטת החיסול מועילה כאשר המקדם של אחד המשתנים זהה (או המקבילה השלילית שלו) בכל המשוואות. היתרון העיקרי של מטריצות מוגדלות הוא שניתן להשתמש בהן כדי לפתור מערכות של שלוש משוואות או יותר במצבים בהם החלפה והסרה הם בלתי אפשריים או בלתי אפשריים.