תוֹכֶן
במתמטיקה חקר המשולשים נקרא טריגונומטריה. כל ערכים לא ידועים של זוויות וצדדים עשויים להתגלות תוך שימוש בזהויות הטריגונומטריות הנפוצות של Sine, Cosine ו- Tangent. זהויות אלו הינן חישובים פשוטים המשמשים להמרת יחסי הצדדים לדרגות זווית. נקראות זוויות לא ידועות זווית תטא וניתן לחשב אותם בדרכים שונות, על סמך צדדים וזוויות ידועים.
משולשים ימניים
כאשר משולש מכיל זווית של 90 מעלות, הוא מכונה א משולש זווית ישרה, וניתן לקבוע את התטא בזווית באמצעות ראשי תיבות SOHCAHTOA.
בפירוק זה מייצג כי סינוס (S) שווה לאורכו של זווית התטא הצדדית הפוכה (O) מחולק באורך ההנפה (H) כך ש- Sin (X) = Opp / Hyp. באופן דומה, הקוסין (C) שווה לאורכו של הצד הסמוך (A) חלקי היפוזה. (ח) Cos (X) = עד / היפ. המשיק (T) שווה להיפך (O) חלקי הסמוך (A). שזוף (X) = Opp / Adj.
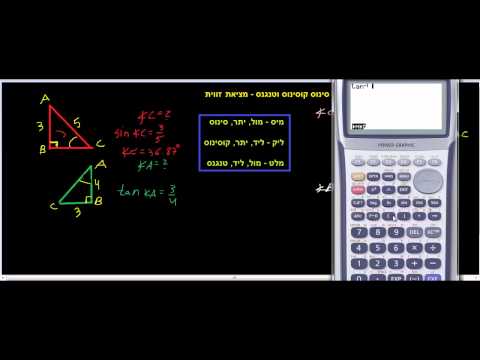
כדי לפתור יחסים אלה באמצעות מחשבון גרף, אתה משתמש בפונקציות הטריגר ההפוכות - הידועות כ ארקסין, ארקוס ו ארקטן - ומיוצג על המחשבון כ- SIN ^ -1, COS ^ -1 ו- TAN ^ -1.
אם אורך הצד הנגדי ידוע כמו גם היפוזה - המתאים ל- SOH בראשי תיבות - השתמש בפונקציה arcsin במחשבון, ואז הזן את שני האורך בצורה חלקית.
לדוגמא: אם לתא הזווית הפוכה בצד השני יש אורך של 4 ולתנוחה האורך 5, הזן את היחס למחשבון כך:
SIN ^ -1 (4/5)
זה אמור להפיק ערך של כ 53.13 מעלות. אם לא, וודא שהמחשבון מוגדר למצב DEGREE ואז נסה שוב.
דיני קנס
אם אין זוויות של 90 מעלות במשולש, ל- SOHCAHTOA אין שום משמעות בפתרון עבור זוויות. עם זאת, אם ידוע זווית ואורך הצד הנגדי שלה, דיני קנס ניתן להשתמש בשיתוף פעולה עם אורך צד ידוע אחר כדי למצוא זוויות חסרות. החוק קובע כי חטא A / a = חטא B / b = חטא C / c.
פירוק זה אומר שהסינוס של זווית המחולק באורך הצד הנגדי שלו עומד ביחס ישיר לסינוס של זווית אחרת המחולק באורך הצד הנגדי שלו. כדי לפתור, יש לבודד את הסינוס של הזווית הלא ידועה על ידי הכפלת שני צידי המשוואה באורך הזווית שמהצד הנגדי.
לדוגמא: חטא A / a = חטא B / b הופך (b * חטא A) / a = חטא B
במחשבון, נתון בצד a = 5, בצד b = 7, ובזווית A = 45 מעלות, זה נתפס כ- SIN ^ -1 ((7 * SIN (45)) / 5). זה נותן לזווית B ערך של כ 81.87 מעלות.
חוק הקוסמינים
ה חוק הקוסמינים פועל על כל המשולשים אך משמש בעיקר במקרים שבהם אורכי כל הצדדים ידועים, אך אף אחת מהזוויות לא ידועה. הנוסחה דומה ל- משפט פיתגורס (a ^ 2 + b ^ 2 = c ^ 2) ומציין c ^ 2 = a ^ 2 + b ^ 2 - 2ab * cos (C). אך למטרות מציאת תטא קל יותר לקרוא כ- cos (C) = (a ^ 2 + b ^ 2 - c ^ 2) / 2ab.
לדוגמה, אם למשולש יש שלושה צדדים בגודל 5, 7 ו 10, הזן ערכים אלה למחשבון הגרף כ- ^ ^ ((5 ^ 2 + 7 ^ 2 - 10 ^ 2) / (2_5_7)). חישוב זה מוציא ערך של כ- 111.80 מעלות.
תרגול לשליטה
דבר שחשוב לזכור הוא שכל המשולשים מורכבים משלוש זוויות שיש להן סכום כולל של 180 מעלות. תרגלו את הטכניקות השונות במשולשים שונים עד שהתהליך מתוודע. לפעמים גילוי תטא זהה לגלות דרך חדשה לעקוף את הבעיה.