כיצד לחשב את המהירות הזוויתית

תוֹכֶן

• יסודות התנועה
• משוואת המהירות הזוויתית
• משוואות תנועה סיבוביות
• כמויות וביטויים קשורים
• מהירות זוויתית לעומת מהירות לינארית

בשיח היומיומי משתמשים לעתים קרובות "מהירות" ו"מהירות "זה בזה. בפיזיקה, לעומת זאת, למונחים אלה יש משמעויות ספציפיות ומובחנות. "מהירות" הוא קצב העקירה של אובייקט בחלל, והוא ניתן רק על ידי מספר עם יחידות ספציפיות (לרוב במטרים לשנייה או מייל לשעה). מהירות, לעומת זאת, היא מהירות המחוברת לכיוון. מהירות, אם כן, נקראת כמות סקלרית, ואילו המהירות היא כמות וקטורית.

כאשר מכונית צונמת לאורך כביש מהיר או בייסבול שורץ באוויר, נמדדת המהירות של חפצים אלה בהתייחסות לקרקע, ואילו המהירות משלבת מידע נוסף. לדוגמה, אם אתה במכונית שנוסעת 70 מייל לשעה בכביש המהיר 95 בחוף המזרחי של ארצות הברית, מועיל לדעת גם אם היא פונה צפונית-מזרחית לכיוון בוסטון או דרומה לכיוון פלורידה. עם הבייסבול, אולי תרצה לדעת אם קואורדינטת ה- y שלה משתנה מהר יותר מקואורדינטת ה- x שלה (כדור זבוב) או אם ההפך הוא הנכון (כונן קו). אך מה עם סיבוב הצמיגים או סיבוב (סיבוב) של הבייסבול כאשר המכונית והכדור נעים לעבר יעדם הסופי? לשאלות מסוג זה, הפיזיקה מציעה את הרעיון של מהירות זוויתית.

יסודות התנועה

הדברים עוברים במרחב פיזי תלת ממדי בשתי דרכים עיקריות: תרגום וסיבוב. תרגום הוא העקירה של כל האובייקט ממקום אחד למקום אחר, כמו מכונית שנוסעת מניו יורק לעיר לוס אנג'לס. סיבוב, לעומת זאת, הוא התנועה המחזורית של אובייקט סביב נקודה קבועה. חפצים רבים, כמו הבייסבול בדוגמה לעיל, מציגים את שני סוגי התנועה בו זמנית; כאשר כדור זבוב נע באוויר מהצלחת הביתית לעבר גדר החוץ, הוא מסתובב בקצב מסוים סביב מרכזו הפרטי.

התיאור של שני סוגים אלה של תנועה מתייחסים כאל בעיות פיזיות נפרדות; כלומר, בעת חישוב המרחק שהכדור עובר באוויר על בסיס דברים כמו זווית השיגור הראשונית שלו והמהירות בה הוא משאיר את העטלף, אתה יכול להתעלם מסיבובו, וכשמחשבים את הסיבוב שלו אתה יכול להתייחס אליו כאל יושב באחת מקום למטרות נוכחיות.

משוואת המהירות הזוויתית

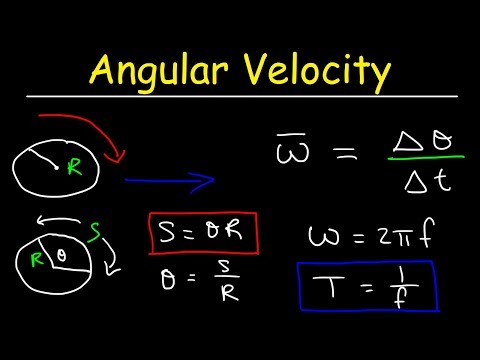
ראשית, כשמדובר על משהו "זוויתי", בין אם מדובר על מהירות או על כמות פיזית אחרת כלשהי, הכיר בכך שמכיוון שאתה מתמודד עם זוויות, אתה מדבר על נסיעה במעגלים או חלקים מהם. אתה עשוי לזכור מגיאומטריה או טריגונומטריה שהיקף המעגל הוא הקוטר שלו פי pi הקבוע, או πd. (הערך של pi הוא בערך 3.14159.) הדבר מתבטא יותר במונחים של רדיוס המעגלים r, שהוא חצי הקוטר, מה שהופך את ההיקף 2πr.

בנוסף, בטח למדת איפשהו בדרך שמעגל מורכב מ- 360 מעלות (360 מעלות). אם אתה מזיז מרחק S לאורך מעגל, כי העקירה הזוויתית θ שווה ל- S / r. מהפכה אחת מלאה, אם כן, נותנת 2πr / r, אשר פשוט משאיר 2π. זה אומר זוויות פחות מ- 360 ° יכולות להתבטא במונחים של pi, או במילים אחרות, כראדיאנים.

כשאתה לוקח את כל חלקי המידע האלה יחד, אתה יכול לבטא זוויות, או חלקים של מעגל, ביחידות שאינן מעלות:

360 ° = (2π) רדיאנים, או

רדיאן 1 = (360 ° / 2π) = 57.3 °,

בעוד שמהירות ליניארית באה לידי ביטוי באורך לכל זמן ליחידה, המהירות הזוויתית נמדדת ברדיאנים לזמן יחידה, בדרך כלל לשנייה.

אם אתה יודע שחלקיק נע בנתיב מעגלי במהירות v ממרחק r ממרכז המעגל, עם הכיוון של v כשהוא תמיד בניצב לרדיוס המעגל, אז ניתן לכתוב את המהירות הזוויתית

ω = v / r,

איפה ω הוא האות היוונית אומגה. יחידות מהירות זוויתית הן רדיאנים בשנייה; אתה יכול גם להתייחס ליחידה זו כאל "שניות הדדיות", מכיוון ש- v / r מניב m / s חלקי m, או s^-1כלומר, רדיאנים הם באופן טכני כמות ללא יחידה.

משוואות תנועה סיבוביות

נוסחת האצה הזוויתית נגזרת באותה דרך חיונית כמו נוסחת המהירות הזוויתית: היא בסך הכל התאוצה הלינארית בכיוון הניצב לרדיוס המעגל (באופן שווה, האצתו לאורך משיק לנתיב המעגלי בכל נקודה) המחולקת לפי רדיוס המעגל או חלק המעגל, שהוא:

α = a_t/ r

זה ניתן גם על ידי:

α = ω / t

מכיוון שתנועה סיבובית, א_t = ωr / t = v / t.

α, כפי שאתה בוודאי יודע, הוא האות היוונית "אלפא". המינוי "t" כאן מציין "משיק".

אולם באופן מוזר, תנועה סיבובית מתהדרת בתאוצה מסוג אחר, המכונה תאוצה צנטריפטלית ("מחפשת מרכז"). זה ניתן בביטוי:

א_ג = v²/ r

תאוצה זו מכוונת אל הנקודה שסביבה מסתובב האובייקט המדובר. זה אולי נראה מוזר, מכיוון שהאובייקט לא מתקרב לנקודה מרכזית זו מאז הרדיוס r מתוקן. חשבו על תאוצה צנטריפטלית כנפילה חופשית בה אין סכנה שהאובייקט יפגע בקרקע, מכיוון שהכוח הנושא את האובייקט אליו (בדרך כלל כוח המשיכה) מתקזז בדיוק על ידי התאוצה המשיקית (הלינארית) שתוארה על ידי המשוואה הראשונה ב הסעיף הזה. אם א_ג לא היו שווים ל א_t, האובייקט היה עף לחלל או בקרוב מתרסק לאמצע המעגל.

כמויות וביטויים קשורים

למרות שבדרך כלל מהירות הזווית מתבטאת, כאמור, ברדיאנים לשנייה, יתכנו מקרים בהם עדיף או נחוץ להשתמש במעלות בשנייה במקום, או להפך, להמיר מעלות לרדיאנים לפני פיתרון בעיה.

נניח שאמרו לכם שמקור אור מסתובב 90 מעלות לשנייה במהירות קבועה. מה המהירות הזוויתית שלה ברדיאנים?

ראשית, זכור כי 2 רדיאנים = 360 °, וקבעו פרופורציה:

360 / 2π = 90 / x

360x = 180π

x = ω = π / 2

התשובה היא חצי רדיאנים של פי שנייה.

אם נאמר לך עוד כי קרן האור טווחה של 10 מטרים, מה יהיה קצה המהירות הקווית של הקורות v, האצתו הזוויתית α והתאוצה המרכזית שלה א_ג?

לפתור עבור v, מלמעלה, v = ωr, כאשר ω = π / 2 ו r = 10m:

(π / 2) (10) = 5π rad / s = 15.7 m / s

לפתור עבור α, פשוט הוסף יחידת זמן נוספת למכנה:

α = 5π rad / s²

(שים לב שהדבר פועל רק לבעיות בהן המהירות הזוויתית קבועה.)

לבסוף, גם מלמעלה, א_ג = v²/ r = (15.7)²/ 10 = 24.65 מ '/ ש².

מהירות זוויתית לעומת מהירות לינארית

בנה על הבעיה הקודמת, דמיין את עצמך בסיבוב שמח גדול מאוד, כזה עם רדיוס בלתי סביר של 10 ק"מ (10,000 מטר). סיבוב עליז זה עושה מהפכה אחת שלמה כל דקה ו- 40 שניות, או כל 100 שניות.

תוצאה אחת של ההבדל בין מהירות זוויתית, שאינה תלויה במרחק המרחק מציר הסיבוב, לבין מהירות מעגלית ליניארית, שאיננה, היא ששני אנשים חווים אותו דבר ω יכול להיות שעבר ניסיון גופני שונה בהרבה. אם אתה נמצא במרחק של מטר מהמרכז אם השבוי הזה, מסיבי, מסיבוב, המהירות הלינארית (המשיקית) שלך היא:

ωr = (2π rad / 100 s) (1 m) = 0.0628 m / s, או 6.29 ס"מ (פחות מ- 3 אינץ ') לשנייה.

אבל אם אתה נמצא על שפת המפלצת הזו, המהירות הקווית שלך היא:

ωr = (2π rad / 100 s) (10,000 m) = 628 m / s. זה בערך 1,406 מייל לשעה, מהיר יותר מכדור. חכה!