
תוֹכֶן
במעגלים חשמליים ניתן יהיה לסדר את אלמנטי המעגל שלהם בסדרה או במקביל. במעגלי סדרה, אלמנטים מחוברים באמצעות אותו ענף שנמצא זרם חשמלי דרך כל אחד מהם אחד אחד. במעגלים מקבילים, לאלמנטים יש ענפים נפרדים משלהם. במעגלים אלה הזרם יכול ללכת בנתיבים שונים לאורך כל הדרך.
מכיוון שהזרם יכול לעבור נתיבים שונים במעגל מקביל, הזרם אינו קבוע לאורך מעגל מקביל. במקום זאת, עבור ענפים המחוברים זה בזה במקביל, ירידת המתח או הפוטנציאל על פני כל ענף הם קבועים. הסיבה לכך היא שהזרם מפיץ את עצמו על פני כל ענף בכמויות שיחסיות הפוך להתנגדות של כל ענף. זה גורם לזרם להיות הגדול ביותר במקום בו ההתנגדות היא הפחותה ולהיפך.
איכויות אלה מאפשרות למעגלים מקבילים לאפשר לטעון דרך שני נתיבים או יותר, והופכים אותו למועמד סטנדרטי בבתים ומכשירים חשמליים באמצעות מערכת כוח יציבה ויעילה. זה מאפשר לחשמל לזרום דרך חלקים אחרים במעגל כאשר חלק פגום או שבור, והם יכולים להפיץ כוח באופן שווה על פני מבנים שונים. ניתן להדגים את המאפיינים האלה באמצעות דיאגרמה ודוגמה למעגל מקביל.
תרשים מעגלים מקבילים
טיפים
דוגמאות למעגלים מקבילים
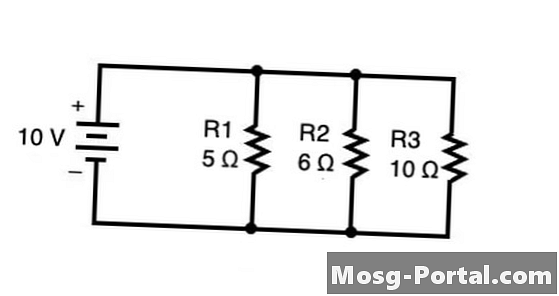
כדי למצוא את ההתנגדות הכוללת של נגדים המסודרים במקביל זה לזה, השתמש בנוסחה 1 / Rסה"כ = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn בו מסוכמת ההתנגדות של כל נגדי בצד ימין של המשוואה. בתרשים לעיל, ניתן לחשב את ההתנגדות הכוללת באו"ם (Ω) באופן הבא:
שים לב שאתה יכול רק "להעיף" את שני צידי המשוואה משלב 3 לשלב 4 כאשר יש רק מונח אחד משני צידי המשוואה (במקרה זה, 1 / Rסה"כ משמאל ו 14/30 Ω בצד ימין).
לאחר שחישבת את ההתנגדות, ניתן לחשב זרם ומתח באמצעות חוק אוהם V = I / R בו V הוא מתח שנמדד בוולט, אני הוא זרם נמדד במגברים, ו ר היא התנגדות באוהמס. במעגלים מקבילים, סכום הזרמים דרך כל נתיב הוא הזרם הכולל מהמקור. ניתן לחשב את הזרם בכל נגדי במעגל על ידי הכפלת התנגדות פעמים מתח נגד הנגד. המתח נשאר קבוע לאורך כל המעגל ולכן המתח הוא המתח של הסוללה או מקור המתח.
מקביל מול סדרת המעגלים
••• סיד חוסיין אתרבמעגלי סדרה, הזרם קבוע לאורך, ירידות מתח תלויות בהתנגדות של כל נגדי וההתנגדות הכוללת היא הסכום של כל נגדי אינדיבידואלי. במעגלים מקבילים המתח הוא קבוע לאורך, הזרם תלוי בכל נגדי וההיפוך של ההתנגדות הכוללת הוא סכום ההיפוך של כל נגדי אינדיבידואלי.
ניתן להשתמש בקבלים ומשרנים כדי לשנות את המטען בסדרות ובמעגלים מקבילים לאורך זמן. במעגל סדרה, סך הכל קיבול של המעגל (ניתן על ידי המשתנה ג), הפוטנציאל של קבל לאחסון מטען לאורך זמן, הוא הסכום ההפוך של ההיפוכים של כל קיבול בודד, וה השראות מוחלטות (אני), כוחם של משרנים לפצות טעינה לאורך זמן, הוא הסכום של כל משרן. לעומת זאת, במעגל מקביל הקיבול הכולל הוא הסכום של כל קבל בודד, וההיפך של השראות הכוללת הוא סכום ההיפוכים של כל השראה פרטנית.
לסדרות ולמעגלים מקבילים יש גם פונקציות שונות. במעגל סדרתי, אם חלק אחד נשבר, הזרם כלל לא יזרום במעגל. במעגל מקביל, פתיחת סניף בודדת עוצרת רק את הזרם באותו הענף. שאר הענפים ימשיכו לעבוד מכיוון שלזרם יש נתיבים מרובים שהוא יכול לעבור ברחבי המעגל.
מעגל מקבילי סדרה

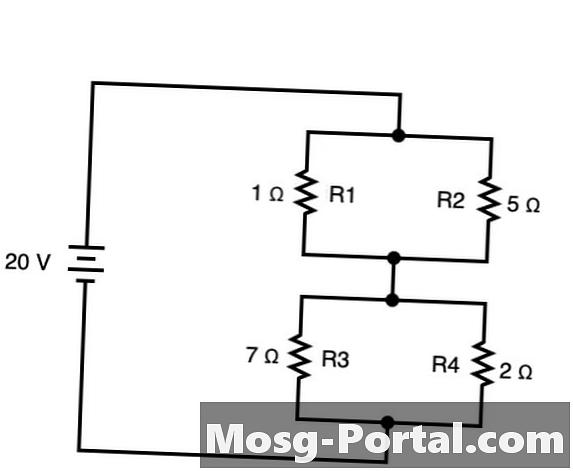
מעגלים שיש להם שני אלמנטים מסועפים המחוברים גם הם כך שזרם זורם בכיוון אחד בין אותם ענפים הם שניהם סדרה ומקבילה. במקרים אלה, באפשרותך להחיל כללים משני הסדרות והמקבילות בהתאם למעגל. בדוגמה לעיל, R1 ו R2 נמצאים במקביל זה לזה R5, וכך גם הם R3 ו R4 כדי ליצור R6. ניתן לסכם אותם במקביל כדלקמן:
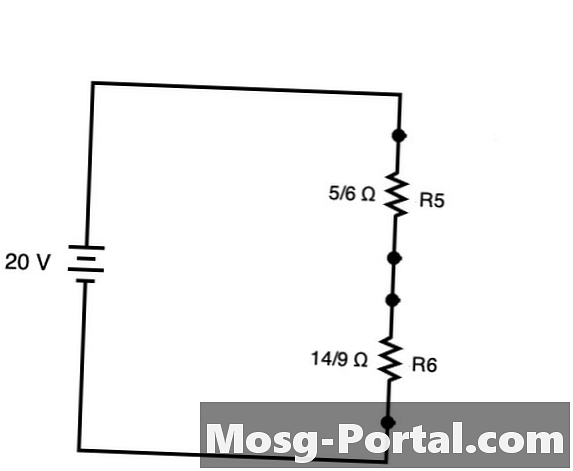
ניתן לפשט את המעגל ליצירת המעגל המוצג ישירות למעלה עם R5 ו R6. ניתן להוסיף שני נגדים אלה ישירות כאילו המעגל היה סדרה.
רסה"כ = 5/6 Ω + 14/9 Ω = 45/54 Ω + 84/54 Ω = 129/54 Ω = 43/18 Ω או בערך 2.38 Ω
עם 20 V ככל שהמתח, חוק אוהם מכתיב כי כל הזרם שווה V / R, או 20V / (43/18 Ω) = 360/43 A או בערך 8.37 א. עם הזרם הכולל הזה, אתה יכול לקבוע את ירידת המתח על פני R5 וגם R6 באמצעות חוק אוהם (V = I / R) גם כן.
ל R5, V5 = 360/43 A x 5/6 Ω = 1800/258 V או בערך 6.98 V.
ל R6, V6 = 360/43 A x 14/9 Ω = 1680/129 V או בערך 13.02 V.
לבסוף, מתח זה יורד עבור R5 ו R6 ניתן לפצל בחזרה למעגלים המקבילים המקוריים כדי לחשב זרם של R1 ו R2 ל R5 ו R2 ו R3 ל R6 באמצעות חוק אוהם.
I1 = (1800/258 V) / 1 Ω = 1800/258 A או על פי 6.98 A._
I2 = (1800/258 V) / 5 Ω = 1500/43 A או בערך 34.88 A._
I3 = (680/129 V) / 7 Ω = 4760/129 א או בערך 36.90 א.
I3 = (680/129 V) / 2 Ω = 1360/129 א או בערך 10.54 א.