כיצד למצוא את התחום של שבר

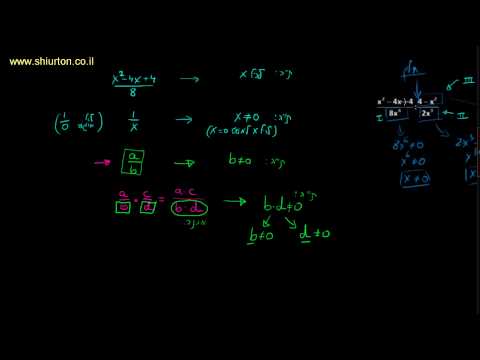
התחום של שבר מתייחס לכל המספרים האמיתיים שהמשתנה הבלתי תלוי בשבר יכול להיות. הכרת אמיתות מתמטיות מסוימות לגבי מספרים אמיתיים ופתרון כמה משוואות אלגברה פשוטות יכולה לעזור לך למצוא את התחום של כל ביטוי רציונלי.

התבונן במכנה של השבר. המכנה הוא המספר התחתון בשבריר. מכיוון שאי אפשר לחלק באפס, המכנה של שבר אינו יכול להיות שווה לאפס. לכן עבור חלק 1 / x, התחום הוא "כל המספרים שאינם שווים לאפס", מכיוון שהמכנה אינו יכול להיות שווה לאפס.

חפש שורשים מרובעים בכל מקום בבעיה, למשל (xrtx x) / 2. מכיוון ששורשים ריבועים עם מספרים שליליים אינם אמיתיים, הערכים שמתחת לסמל השורש הריבועי חייבים להיות גדולים מאפס או שווה להם. בבעיית הדוגמא שלנו, התחום הוא "כל המספרים הגדולים או שווים לאפס."

הגדר בעיית אלגברה לבידוד המשתנה בשברים מורכבים יותר.

לדוגמה: כדי למצוא את התחום של 1 / (x ^ 2 -1), הגדר בעיית אלגברה כדי למצוא את הערכים של x שיגרום למכנה להיות שווה 0. X ^ 2-1 = 0 X ^ 2 = 1 Sqrt (x ^ 2) = Sqrt 1 X = 1 או -1. התחום הוא "כל המספרים שאינם שווים ל -1 או -1."

כדי למצוא את התחום של (sqrt (x-2)) / 2, הגדר בעיית אלגברה כדי למצוא את הערכים של x שיגרום לערך מתחת לסמל השורש המרובע להיות פחות מ 0. x-2 <0 x < 2 התחום הוא "כל המספרים הגדולים או שווים ל -2."

כדי למצוא את התחום של 2 / (sqrt (x-2)), הגדר בעיית אלגברה כדי למצוא את הערכים של x שיגרמו לערך מתחת לסמל השורש המרובע להיות פחות מ 0 והערכים של x שיגרמו המכנה לשווה ל -0.

x-2 <0 x-2 <0 x <2

ו

ריבוע (x-2) = 0 (sqrt (x-2)) ^ 2 = 0 ^ 2 x-2 = 0 x = 2

התחום הוא "כל המספרים הגדולים מ -2."