כיצד גורמים פולינומים עם מקדמים

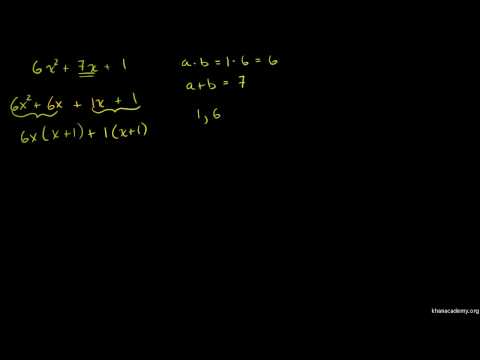
פולינום הוא ביטוי מתמטי המורכב ממשתנים ומקדמים הבנויים יחד תוך שימוש בפעולות חשבון בסיסיות, כגון כפל ותוספת. דוגמה לפולינום הוא הביטוי x ^ 3 - 20x ^ 2 + 100x. תהליך הפקטורציה של פולינום פירושו פישוט פולינום לצורה הפשוטה ביותר שהופכת את האמירה לאמיתה. הבעיה של פקטורציה של פולינומים מתעוררת לעיתים קרובות בקורסים של פרוקלקול, אך ניתן לבצע פעולה זו עם מקדמים בכמה צעדים קצרים.

הסר את הגורמים השכיחים מהפולינום, במידת האפשר. כדוגמה, למונחים בפולינום x ^ 3 - 20x ^ 2 + 100x יש את הגורם המשותף x. לכן ניתן לפשט את הפולינומם ל- x (x ^ 2 - 20x + 100).

קבע את צורת התנאים שנשארו לעבוד עליהם. בדוגמה שלמעלה, המונח x ^ 2 - 20x + 100 הוא ריבועי עם מקדם מוביל של 1 (כלומר המספר מול משתנה הכוח הגבוה ביותר, שהוא x ^ 2, הוא 1), ולכן יכול להיפתר בשיטה ספציפית כדי לפתור בעיות מסוג זה.

הגדר את יתר התנאים. ניתן לחשב את הפולינום x ^ 2 - 20x + 100 לצורה x ^ 2 + (a + b) x + ab, שניתן גם לכתוב כ- (x - a) (x - b), כאשר a ו- b הם מספרים שייקבעו. לפיכך, הגורמים נמצאים על ידי קביעת שני מספרים a ו- b שמסתכמים ל -20 ושווים ל 100 כאשר מוכפלים יחד. שני מספרים כאלה הם -10 ו- -10. הצורה המובנית של פולינום זה היא אז (x - 10) (x - 10), או (x - 10) ^ 2.

כתוב את הצורה המעובדת במלואה של הפולינום המלא, כולל כל המונחים שהוקמו. בסיכום הדוגמה לעיל, הפולינום x ^ 3 - 20x ^ 2 + 100x נבדק לראשונה על ידי פקטורינג x, נותן x (x ^ 2 - 20x +100), ופקטורציה של הפולינום בתוך הסוגריים נותן x (x - 10) ^ 2, שהיא הצורה המאוחדת במלואה של הפולינום.